∫ e ( x 2 + 7 x) ( 2 x + 7) d x. Finding an antiderivative of an exponential function.
Integration Rules For Exponential. The derivative of the exponential function ,$e^x$, is simply $e^x$ itself. Understanding $\boldsymbol {\int e^x \phantom {x}dx = e^x +c}$.
Ex 2 Derivatives Involving the Exponential Function with From youtube.com
The exponential function, is its own derivative and its own integral. Solved example of integrals of exponential functions. Properties of the natural exponential function:
Ex 2 Derivatives Involving the Exponential Function with
, where , and , where a is any positive constant not equal to 1 and is the natural (base e) logarithm of a. ∫ e ( x 2 + 7 x) ( 2 x + 7) d x. Exponential and then whatever is left is dv. Here are a number of highest rated integration of exponential function pictures upon internet.
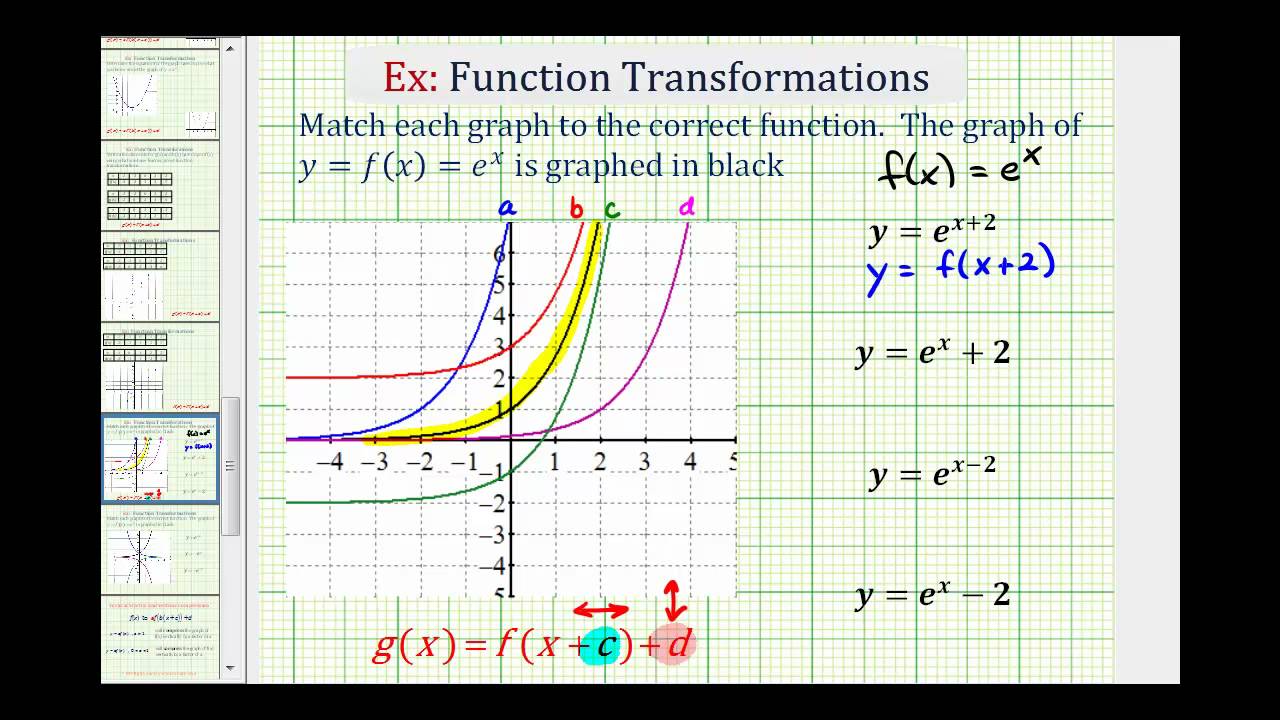Source: youtube.com
First, we must identify a section within the. We identified it from honorable source. ∫ e x d x = e x + c , ∫ a x d x = ln ( a ) a x + c. Earlier, we had the derivative rule. ∫ ( 2 x + 7) e x 2 + 7 x d x.
Source: youtube.com
Since the derivative of ex is e x;e is an antiderivative of ex:thus z exdx= ex+ c recall that the exponential function with base ax can be represented with the base eas elnax = e xlna:with substitution u= xlnaand using the above formula for the integral of e;we have that z axdx= z An indefinite integral computes the family of.
Source: slideshare.net
Properties of the natural exponential function: Observe the following decreasing pattern: ∫ e x x d x = e x + c ∫ a x x d x = a x ln. Here are a number of highest rated exponential integral table pictures on internet. We can solve the integral.
