49+ Integration Of Square Root Of Tanx

Stack exchange network stack exchange network consists of 178 q&a communities including stack overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build.

Integration Of Square Root Of Tanx. Substitution , followed by partial fractions. I will update this answer as i go.

Example 41 Evaluate integral [root cot x + root tan x] dx From teachoo.com

Ex 7.2, 34integrate √(tan⁡𝑥 )/sin⁡〖𝑥 cos⁡𝑥 〗 simplifying the function √(tan⁡𝑥 )/sin⁡〖𝑥 cos⁡𝑥 〗 = √(tan⁡𝑥 )/(sin⁡〖𝑥 cos⁡𝑥 〗. To integrate \displaystyle\int\sqrt[n]{\tan x}, dx\tag*{} let’s first make the generalized substitution u=\left(\tan x\right)^{1/n}. The integration of secant squared of angle x function with respect to x is equal to sum of the tan of angle x and the constant of.

inalienable rights def idee peinture chambre verte inelastic demand and elastic supply tax inalienable rights definition government

Example 41 Evaluate integral [root cot x + root tan x] dx

Just follow orion�s thread to see how it is done. Derivatives derivative applications limits integrals integral applications integral approximation series ode multivariable calculus laplace transform taylor/maclaurin series fourier series functions line equations functions arithmetic & comp. Nothing further can be done with this topic. ⇒ integral ∫ 2t 2 / (1 + t 4) dt.

Source: brainly.in

As djc told you, you may write 1+tan2x using a common denominator as cos2x+sin2x cos2x = 1 cos2x so the square root of it is simply cosx. $$\int\sqrt{\tan x};\mathrm{d}x = \int\frac{2u^2}{u^4+1};\mathrm{d}u$$ you. Substitution , followed by partial fractions. Please check the expression entered or try another topic. Nothing further can be done with this topic.

Source: teachoo.com

(step 1.) use the substitution, and the integral becomes: Thus $\mathrm{d}x = \dfrac{2u;\mathrm{d}u}{u^4 + 1}$. $\int \sqrt{\tan (x)}dx $ let $\tan(x)=t^{2}$ then $dx$ will become $\frac{2t}{1+t^{4}}$ hence $\int \sqrt{\tan (x)}dx =\int\frac{2t}{1+t^4} dt. $$\int\sqrt{\tan x};\mathrm{d}x = \int\frac{2u^2}{u^4+1};\mathrm{d}u$$ you. Evaluate integral of square root of tan (x)sec (x)^4 with respect to x.

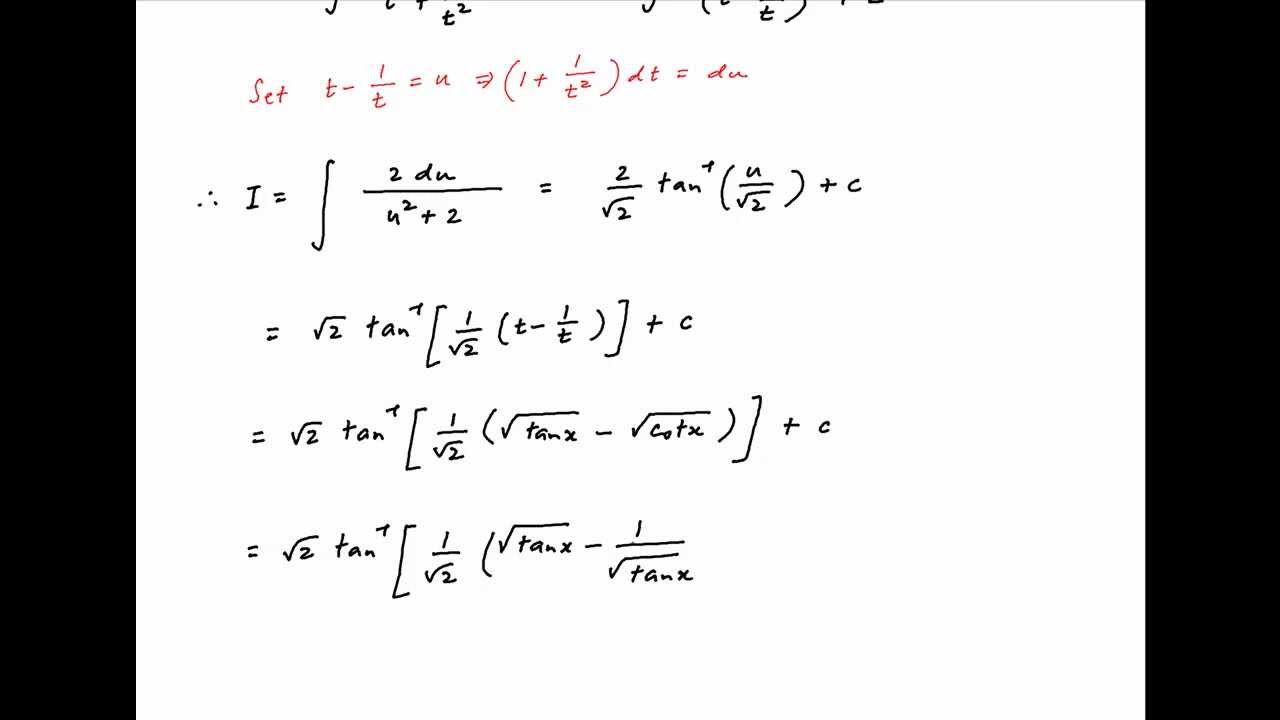Source: youtube.com

(step 2.) we try to factorise the denominator. Substitution , followed by partial fractions. ⇒ integral ∫ 2t 2 / (1 + t 4) dt. Thus $2u;\mathrm{d}u = \sec^2 x;\mathrm{d}x = (u^4 + 1)\mathrm{d}x$. Since the derivative of a constant is 0, indefinite integrals are defined only up to an arbitrary constant.

Source: thewaythetruthandthelife.net

The indefinite integral of , denoted , is defined to be the antiderivative of. ⇒ integral ∫ 2t 2 / (1 + t 4) dt. ∫ √tan(x)sec4 (x)dx ∫ tan ( x) sec 4 ( x) d x. Integration of tan square x will be. To integrate \displaystyle\int\sqrt[n]{\tan x}, dx\tag*{} let’s first make the generalized substitution u=\left(\tan x\right)^{1/n}.

Source: teachoo.com

$$\int\sqrt{\tan x};\mathrm{d}x = \int\frac{2u^2}{u^4+1};\mathrm{d}u$$ you. The indefinite integral of , denoted , is defined to be the antiderivative of. This intimidating integration of square root of tanx can be solved by distinct techniques. To integrate \displaystyle\int\sqrt[n]{\tan x}, dx\tag*{} let’s first make the generalized substitution u=\left(\tan x\right)^{1/n}. Evaluate integral of 1/ ( square root of tan (x)) with respect to x.

Source: math.stackexchange.com

⇒ sec 2 x dx = 2t dt. Please check the expression entered or try another topic. $\int \sqrt{\tan (x)}dx $ let $\tan(x)=t^{2}$ then $dx$ will become $\frac{2t}{1+t^{4}}$ hence $\int \sqrt{\tan (x)}dx =\int\frac{2t}{1+t^4} dt. $$\int\sqrt{\tan x};\mathrm{d}x = \int\frac{2u^2}{u^4+1};\mathrm{d}u$$ you. Stack exchange network stack exchange network consists of 178 q&a communities including stack overflow , the largest, most trusted online community.