49++ Integration Of Root Tanx Dx

I = 1 2(tan−1u − 1 2 ln(1 +u2) + ln(1 + u)) +c. Example 36→ chapter 7 class 12 integrals (term 2) serial order wise

Integration Of Root Tanx Dx. Ex 7.2, 1 ex 7.2, 2 ex 7.2, 3 important. ⇒ sec 2 x dx = 2t dt.

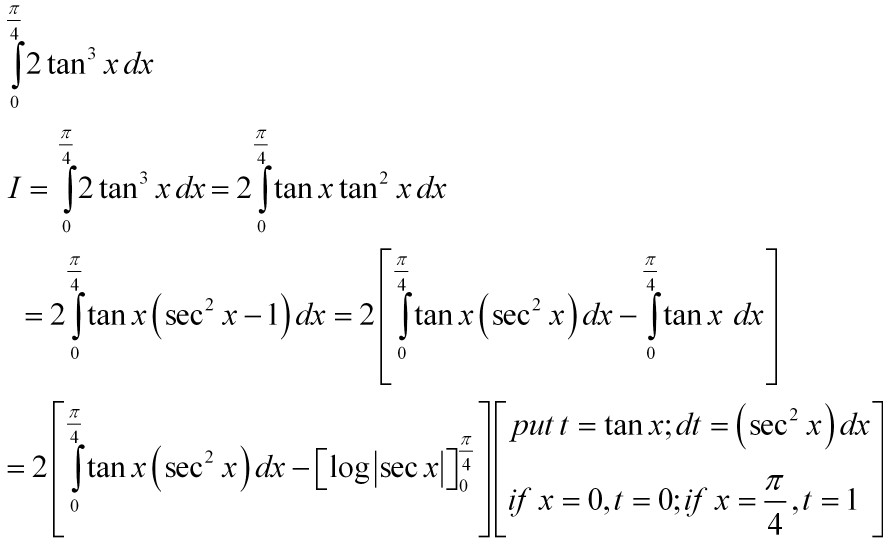tan inverse root (x/1+x squares) Brainly.in From brainly.in

Ex 7.2, 34→ chapter 7 class 12 integrals (term 2) serial order wise; Now, we can easily reach to the final answer as follows. Apply the substitution tanx = u:

hibiscus exterieur plantation isolant acoustique plafond isover joint porte de garage sectionnelle novoferm joint de porte voiture 206

tan inverse root (x/1+x squares) Brainly.in

Please like and subscribe my youtube channel #12thmath #11thmath #integrationofmiscellaneoussubstitutions #calculus #iit #integration #integral thank you wat. Ex 7.2, 34integrate √(tan⁡𝑥 )/sin⁡〖𝑥 cos⁡𝑥 〗 simplifying the function √(tan⁡𝑥 )/sin⁡〖𝑥 cos⁡𝑥 〗 = √(tan⁡𝑥 )/(sin⁡〖𝑥 cos⁡𝑥 〗. [math]i = \displaystyle \int \dfrac{\sqrt{\tan x}}{\sin 2x} \cdot dx[/math] [math]\text{let } t = \tan x \implies dx = \dfrac{dt}{1+t^2}; But its lenghty i will try to minimze the solution further.

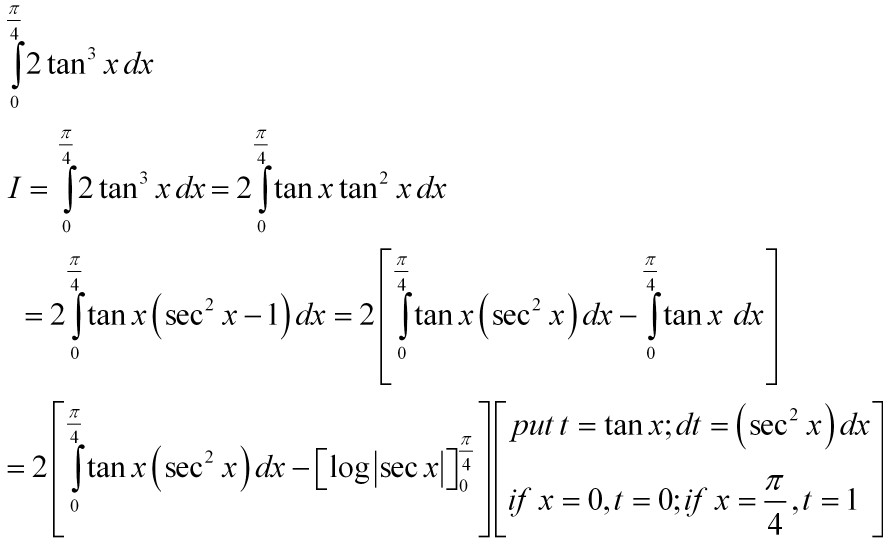Source: keral2008.blogspot.com

Now, we can easily reach to the final answer as follows. Example 1 (i) example 1 (ii) example 1 (iii) example 2 (i). ⇒ integral ∫ 2t 2 / (1 + t 4) dt. Show activity on this post. ⇒ integral ∫ 2t 2 / (1 + t 4) dt.

Source: brainly.in

Let tan x = t 2. I = ∫ 1 (1 +u2)(1 +u) du. ⇒ dx = [2t / (1 + t 4 )]dt. As already mentioned in some answers, let t 2 = tan. There will be always trade off between complexity and instructiin required.

Source: ocw.uwc.ac.za

I = ∫ 1 (1 +u2)(1 +u) du. ⇒ sec 2 x dx = 2t dt. ⇒ integral ∫ 2t 2 / (1 + t 4) dt. I = 1 2(tan−1u − 1 2 ln(1 +u2) + ln(1 + u)) +c. Let tan x = t 2.

Source: teachoo.com

I = ∫ 2 t 2 d t t 4 + 1 = ∫ 2 d t t 2 + 1 t 2 = ∫ ( 1 + 1 t 2) + ( 1 − 1 t 2) d t t 2 + 1 t 2. X 2 t d t = sec 2. Example 1 (i) example 1 (ii).