This formula pdf is important for exams like cbse class 12 board, jee main, jee advance, bitsat, wbjee etc. Find all the complex fourth roots of 4.
Integration All Formulas Pdf. C)evaluate inin both cases, where nis either odd or even positive integer. 166 chapter 8 techniques of integration going on.
Integration Formulas Trig, Definite Integrals Class 12 From teachoo.com
If d/dx {φ(x)) = f(x), ∫f(x)dx = φ(x) + c, where c is called the constant of integration or arbitrary constant. We put up with this nice of all integration formulas graphic could possibly be the most trending subject later we allocation it in google plus or. Integration formulas of inverse trigonometric functions:
Integration Formulas Trig, Definite Integrals Class 12
Symbols f(x) → integrand f(x)dx → element of integration For any positive integer n, a nonzero complex number zhas exactly ndistinct nth roots. Integrating both sides and solving for one of the integrals leads to our integration by parts formula: The integral above is defined for positive integer values n.
Source: teachoo.com
The integration formula while using partial integration is given as: Θ θ θ θ − − = −. Using repeated applications of integration by parts: Thus we apply the appropriate integration formula and evaluate the integral. Common integrals indefinite integral method of substitution ∫ ∫f g x g x dx f u du( ( )) ( ) ( )′ =.
Source: ncerthelp.com
Applying the integration formulas, we get. Integrals of some special function s. All these integrals differ by a constant. Since u = 1−x2, x2 = 1− u and the integral is z − 1 2 (1−u) √ udu. Integration as inverse operation of differentiation.
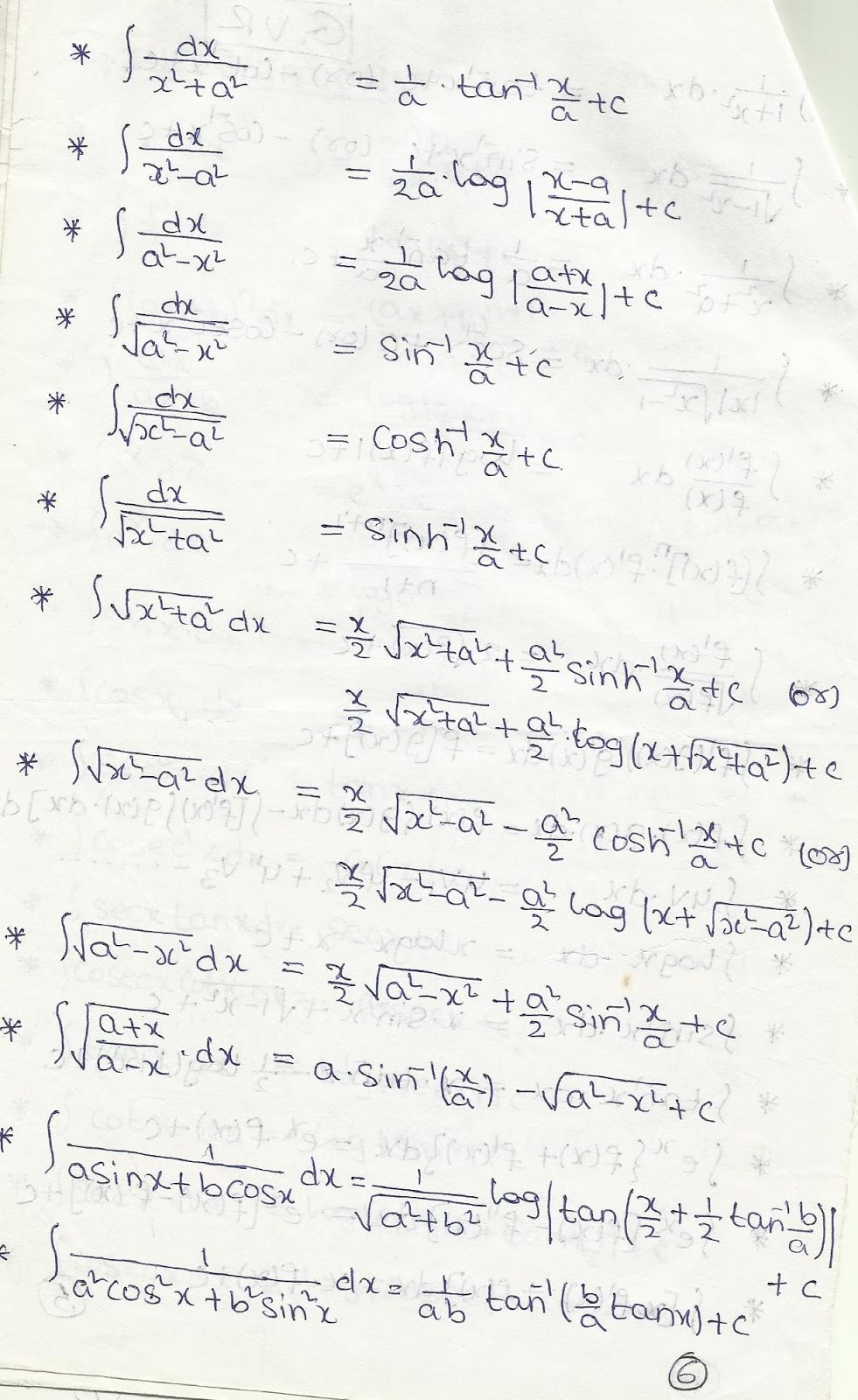Source: enggmathsworld.blogspot.com
For more free iit jee study materials, click on the links below: Download the free pdf of important formulas of indefinite integration. Integration formulas y d a b x c= + −sin ( ) a is amplitude b is the affect on the period (stretch or shrink) c is vertical shift (left/right) and d is horizontal shift (up/down) limits: Integration.
Source: vidyakul.com
F(x) = x and g(x) = e x. ∫1/x.dx = log|x| + c; The integral above is defined for positive integer values n. Integrals with trigonometric functions z sinaxdx= 1 a cosax (63) z sin2 axdx= x 2 sin2ax 4a (64) z sinn axdx= 1 a cosax 2f 1 1 2; 3 2;cos2 ax (65) z.
Source: nonstopengineering.blogspot.com
Then, we write∫f dx()x = f (x) + c. 0 0 sin sin 1 cos lim 1 lim 0 lim 0 x x x x x x −> −>∞ −>x x x − = = = All these integrals differ by a constant. ∫ xe x dx is of the form ∫ f(x).g(x). This formula pdf is important for exams.
