50++ Integral Of Sine Squared Of X

Lets understand how we arrived at the solution. We can rewrite this as the indefinite integral.

Integral Of Sine Squared Of X. We intend to travel a simple path from 0 to x, but we end up with a smaller percentage instead. Its submitted by running in the best field.

![mixture integral of { arcsin(sqrt(x)) arccos(sqrt(x mixture integral of { [ arcsin(sqrt(x)) arccos(sqrt(x From keral2008.blogspot.com

Let’s understand how we arrived at the solution. Because of the first characteristic, there is no elementary antiderivative and therefore we can’t simply plug the. I = z 1 − cos2(x) k cosn(x) sin(x) dx.

idee peinture chambre fille im good regardless quotes idee salle de bain avec baignoire dangle interrupteur schneider odace avec voyant

mixture integral of { [ arcsin(sqrt(x)) arccos(sqrt(x

Now, ∫π 20log2(sin(x))dx = ∫1 0 log2(t) √1 − t2dt. Sometimes an approximation to a definite integral is desired. And now you take all these cosines and you multiply them together and you see what you�ve got. There is a procedure to compute integrals of the form i = z sinm(x) cosn(x) dx.

Source: tomsmath.com

We will use the concept of cos double angle formula for integration of sin square. Integrating each term of the series gives you an infinite series for the integral of sin(x)/x: Integration of sin squared x. F ( x )=sin ( x )/ x; Now, ∫π 20log2(sin(x))dx = ∫1 0 log2(t) √1 − t2dt.

Source: pinterest.com

We identified it from trustworthy source. This is pretty straight forward, now this is going to be u to the third over three minus u. I = ∫ cos 2 x d x. (a) if m = 2k +1, (odd), then sin(2k+1)(x) = sin2(x) k sin(x); This integral cannot be evaluated by the direct formula of integration, so using the.

Source: youtube.com

Here are a number of highest rated integral sin 2x pictures on internet. The integration is of the form. Today we have a tough integral: The latter form can be integrated by means of ∫10 ts − 1 √1 − t2dt = 1 2b(1 2, s 2) = √πγ(s 2) 2γ(s + 1 2) now differentiate with respect to s.

Source: youtube.com

2 x 2, we have. (a) if m = 2k +1, (odd), then sin(2k+1)(x) = sin2(x) k sin(x); Let’s understand how we arrived at the solution. Because of the first characteristic, there is no elementary antiderivative and therefore we can’t simply plug the. I = z 1 − cos2(x) k cosn(x) sin(x) dx.

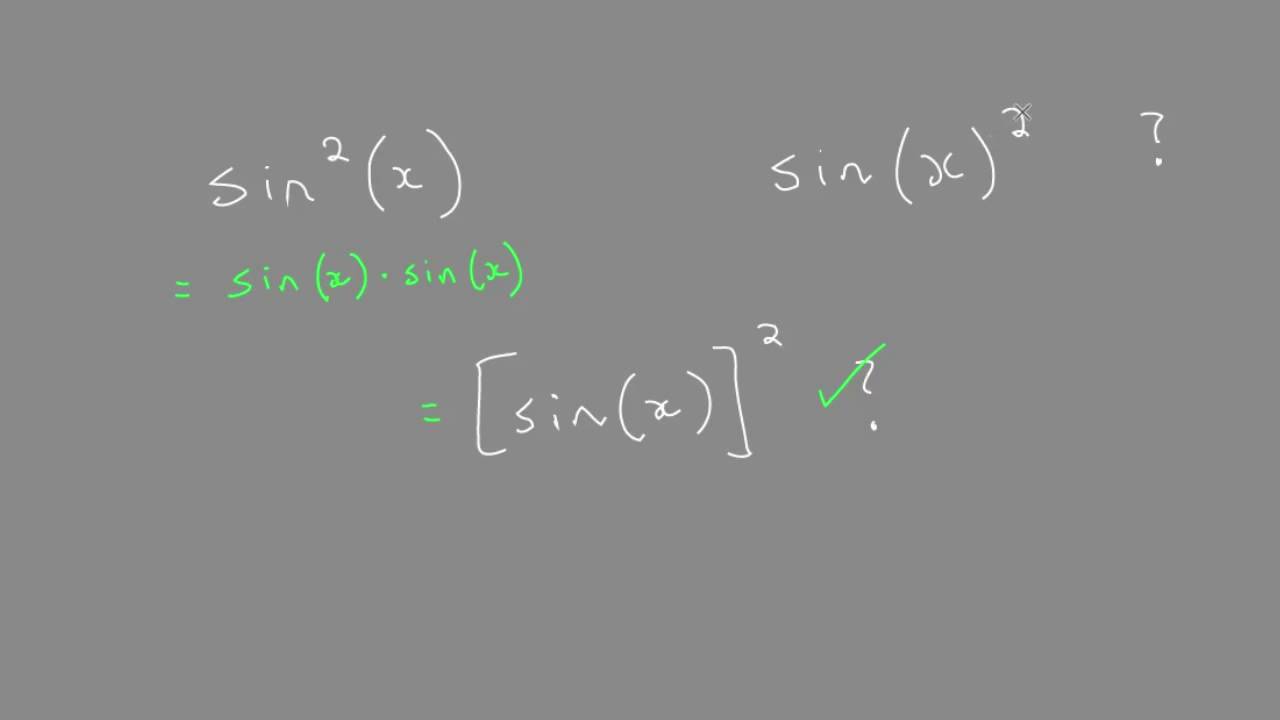Source: youtube.com

Not only is this a special integral (the sine integral si ( x )), but it also goes from 0 to infinity! 6 \times \arctan \tan \log: An integral that is a rational function of the sine and cosine can be evaluated using bioche�s rules. ( x) d x = ( − c o s ( π)) − ( −.

Source: tomsmath.com

If we divide this by x, we can obtain a power series expansion for sin(x)/x: This is going to be equal to the integral of sine x times, well, times sine squared x, which is 1 minus cosine squared x, times cosine x to the minus second power dx. A common way to do so is to place thin rectangles.

Source: slideserve.com

This integral cannot be evaluated by the direct formula of integration, so using the trigonometric identity of half angle sin 2 x. Because $\sin(x)$ is usually less than 100%). I = ∫ sin 2 x d x. C2π 8 + π3 24 + cπ 4 ψ(1 2) + π 8ψ(1 2)2 = π3 24 + π 2log(2)2. Integration of sin.

![mixture integral of { arcsin(sqrt(x)) arccos(sqrt(x Source: keral2008.blogspot.com

So we�d expect something like 0.75x. I integrals of tangents and secants. We will use the concept of cos double angle formula for integration of sin square. Instead of sine squared x we�re saying sine is the same thing as u so we can rewrite that as, u squared minus u to the fourth times du. Now, ∫π 20log2(sin(x))dx =.