In this tutorial we shall derive the integral of sine squared x. The integration is of the form.
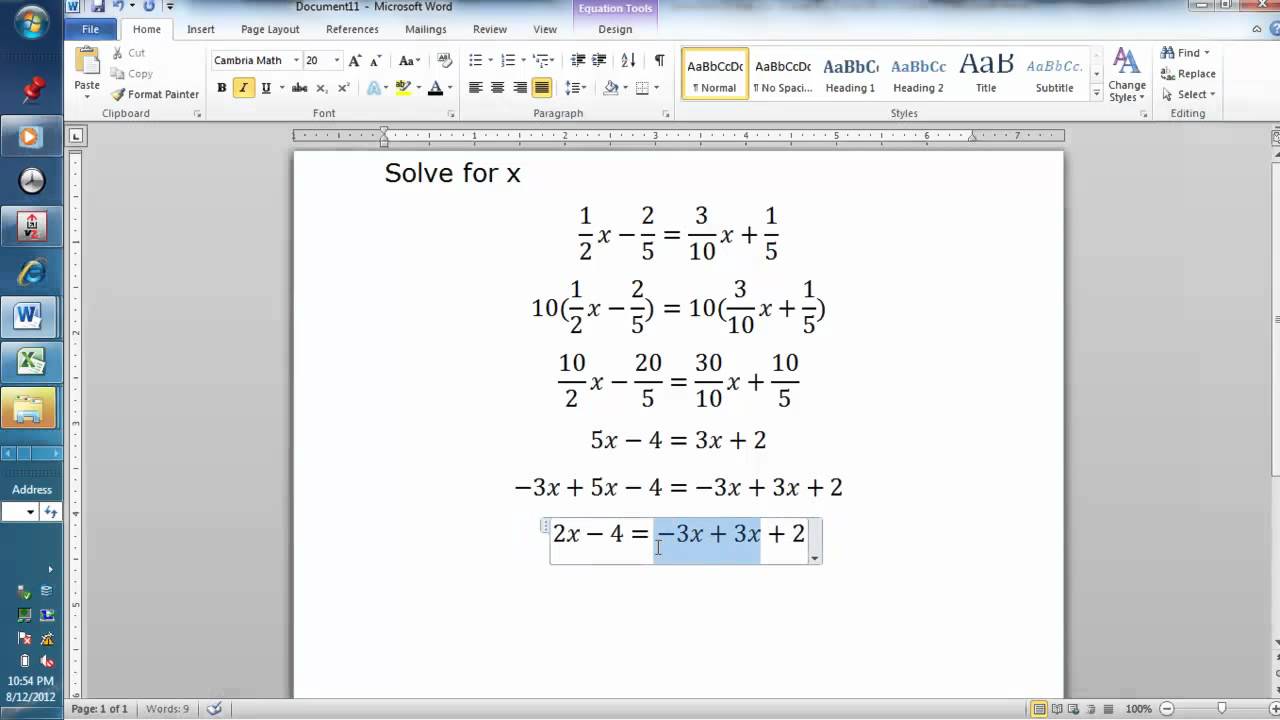
Integral Of Sin Squared 2X. We know that $$∫sin x = − cos x + c$$ hence on substituting, equation (i) becomes $$∫sin 2x dx = ½ ∫sin(u) du$$ $$∫sin 2x dx = ½. Because 1/2 is a constant, we can remove it from the integration to make the calculation simpler.
Trigonometric Identities sin^2(x), cos^2(x), tan^2(x From youtube.com
We recall the double angle formulae and rearrange it for sin 2 x. Sin 2x = (2 sin x cos 2 x)/ (cos x) = 2 (sin x/cosx ) · (cos 2 x) we know that sin x/cos x = tan x and cos x = 1/ (sec x). Its submitted by running in the best field.
Trigonometric Identities sin^2(x), cos^2(x), tan^2(x
We recall the pythagorean identity and rearrange it for cos 2 x. For sin 2 (x), we will use the cos double angle formula: Here are a number of highest rated integral sin 2x pictures on internet. We recall the double angle formulae and rearrange it for sin 2 x.
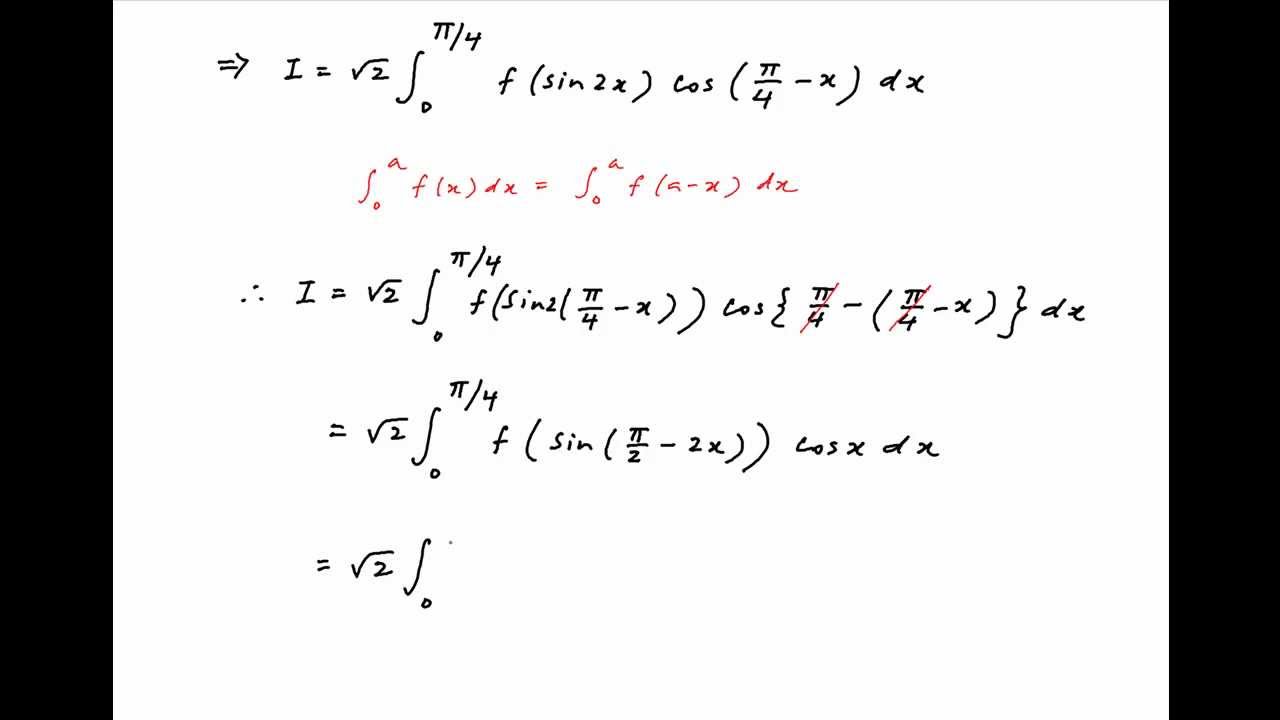Source: youtube.com
For this, let us start with the sin 2x formula. X^ {\msquare} \log_ {\msquare} \sqrt {\square} \nthroot [\msquare] {\square} \le. Here are a number of highest rated integral sin 2x pictures on internet. To integrate sin^22x, also written as ∫sin 2 2x dx, sin squared 2x, (sin2x)^2, and sin^2 (2x), we start by considering standard trig identities to simplify the.
Source: seonegativo.com
We recall the pythagorean identity and rearrange it for cos 2 x. Multiply and divide by cos x. ( x) d x = ( − c o s ( π)) − ( − c o s ( 0)) = 2. To integrate sin^22x, also written as ∫sin 2 2x dx, sin squared 2x, (sin2x)^2, and sin^2 (2x), we start by.
Source: youtube.com
We substitute the cos 2 x expression into the double angle formulae. I = ∫ sin 2 x d x. For sin 2 (x), we will use the cos double angle formula: Here are a number of highest rated integral sin 2x pictures on internet. Because 1/2 is a constant, we can remove it from the integration to make the.
Source: youtube.com
Use the power rule (ab)n = anbn ( a b) n = a n b n to distribute the exponent. Its submitted by running in the best field. A common way to do so is to place thin rectangles under the curve and add the signed areas together. This means ∫π 0 sin(x)dx= (−cos(π))−(−cos(0)) =2 ∫ 0 π sin. Multiply.
Source: youtube.com
We identified it from trustworthy source. This calculus video tutorial explains how to find the integral of sin^2x using power reducing formulas of sine.integration by parts problems: We will use the concept of cos double angle formula for integration of sin square. We substitute the cos 2 x expression into the double angle formulae. We recall the pythagorean identity and.
